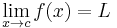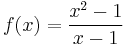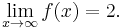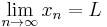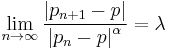Limit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. Limits are essential to calculus (and mathematical analysis in general) and are used to define continuity, derivatives and integrals.
The concept of the limit of a function is further generalized to the concept of topological net, while the limit of a sequence is closely related to limit and direct limit in category theory.
In formulas, limit is usually abbreviated as lim as in lim(an) = a or represented by the right arrow (→) as in an → a.
Contents |
Limit of a function
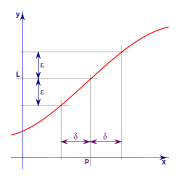
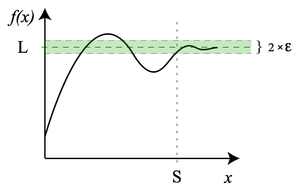
Suppose f(x) is a real-valued function and c is a real number. The expression
means that f(x) can be made to be as close to L as desired by making x sufficiently close to c. In that case, we say that "the limit of f of x, as x approaches c, is L". Note that this statement can be true even if f(c) ≠ L. Indeed, the function f(x) need not even be defined at c.
For example, if
then f(1) is not defined, yet as x approaches 1, f(x) approaches 2:
| f(0.9) | f(0.99) | f(0.999) | f(1.0) | f(1.001) | f(1.01) | f(1.1) |
| 1.900 | 1.990 | 1.999 | ⇒ undef ⇐ | 2.001 | 2.010 | 2.100 |
Thus, f(x) can be made arbitrarily close to the limit of 2 just by making x sufficiently close to 1.
Karl Weierstrass formalized the definition of the limit of a function into what became known as the (ε, δ)-definition of limit in the 19th century.
In addition to limits at finite values, functions can also have limits at infinity. For example, consider
- f(100) = 1.9900
- f(1000) = 1.9990
- f(10000) = 1.9999
As x becomes extremely large, the value of f(x) approaches 2, and the value of f(x) can be made as close to 2 as one could wish just by picking x sufficiently large. In this case, we say that the limit of f(x) as x approaches infinity is 2. In mathematical notation,
Limit of a sequence
Consider the following sequence: 1.79, 1.799, 1.7999,... We could observe that the numbers are "approaching" 1.8, the limit of the sequence.
Formally, suppose x1, x2, ... is a sequence of real numbers. We say that the real number L is the limit of this sequence and we write
to mean
- For every real number ε > 0, there exists a natural number n0 such that for all n > n0, |xn − L| < ε.
Intuitively, this means that eventually all elements of the sequence get as close as we want to the limit, since the absolute value |xn − L| is the distance between xn and L. Not every sequence has a limit; if it does, we call it convergent, otherwise divergent. One can show that a convergent sequence has only one limit.
The limit of a sequence and the limit of a function are closely related. On one hand, the limit of a sequence is simply the limit at infinity of a function defined on natural numbers. On the other hand, a limit of a function f at x, if it exists, is the same as the limit of the sequence xn = f(x + 1/n).
Convergence and fixed point
A formal definition of convergence can be stated as follows. Suppose 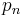 as
as 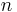 goes from
goes from 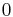 to
to 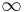 is a sequence that converges to a fixed point
is a sequence that converges to a fixed point 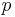 , with
, with 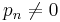 for all
for all 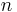 . If positive constants
. If positive constants 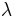 and
and 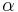 exist with
exist with
then 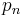 as
as 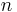 goes from
goes from 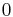 to
to 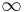 converges to
converges to 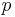 of order
of order 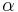 , with asymptotic error constant
, with asymptotic error constant 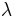
Given a function 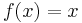 with a fixed point
with a fixed point 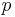 , there is a nice checklist for checking the convergence of p.
, there is a nice checklist for checking the convergence of p.
- 1) First check that p is indeed a fixed point:
- 2) Check for linear convergence. Start by finding
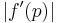 . If....
. If....
![\left | f^\prime (p) \right | \in (0,1]](/I/155216d909029a4cf6c0cffecd3f7eb6.png) |
then we have linear convergence |
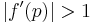 |
series diverges |
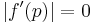 |
then we have at least linear convergence and maybe something better, we should check for quadratic |
- 3) If we find that we have something better than linear we should check for quadratic convergence. Start by finding
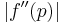 If....
If....
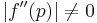 |
then we have quadratic convergence provided that 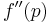 is continuous is continuous |
 |
then we have something even better than quadratic convergence |
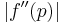 does not exist does not exist |
then we have convergence that is better than linear but still not quadratic |
Topological net
All of the above notions of limit can be unified and generalized to arbitrary topological spaces by introducing topological nets and defining their limits.
An alternative is the concept of limit for filters on topological spaces.
Limit in category theory
See also
- Limit of a function
- Limit of a sequence
- One-sided limit
- Squeeze theorem
- List of limits
- Table of limits
Notes
- ↑ Numerical Analysis, 8th Edition, Burden and Faires, Section 2.4 Error Analysis for Iterative Methods